Hi Carol.

Cubic yards is a unit of volume. You can calculate the volume of stone you need if you know the area and the depth. You didn't mention the depth, so I'll use 1 inch depth and you can multiply the final answer by the number of inches you really want. Here is a diagram of what you are describing:

And below I've drawn the geometric sketch of the surface.

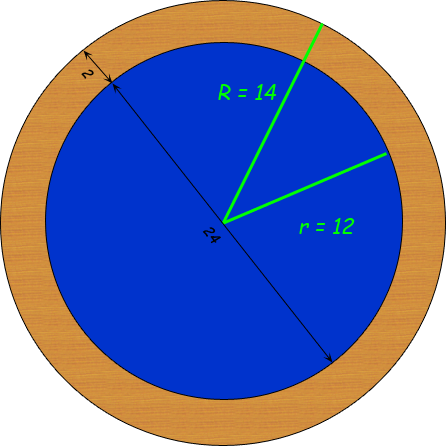If the diameter of the round pool is 24 ft, then its radius is 12 ft. Since the width of the edging is 2 ft, the radius of the circle for the outside of the edging is 2 ft more than the pool's radius. So we have two radii.

We need the area represented as the ring (mathematicians call this an annulus). The area of this ring is just the area of the big circle minus the area of the small circle.

Since the area of a circle is calculated as π r² , the area of the ring is

A = πR² - πr² .

The volume is this area times the depth (d).

V = d ( πR² - πr² ).

Before we put actual numbers into the equation, we have to make sure we are using compatible units. Since you ultimately want cubic yards, we should first convert all the measurements to yards:

d = 1 inch = 1/36 yards,
R = 14 ft = 14/3 yards, and
r = 12 ft = 4 yards.

Now we can use these in our calculations. Remember that π is about 3.1416.

V = (1/36) ( π (14/3)² - π (4)² )
V = 0.5 cubic yards for each inch of depth

So for every inch of depth, you'll need half a cubic yard.

Hope this helps,
Stephen La Rocque.