Hi Cecelia.

That sounds like an big aquarium. Based on your measurements, I think this sketch shows the situation:

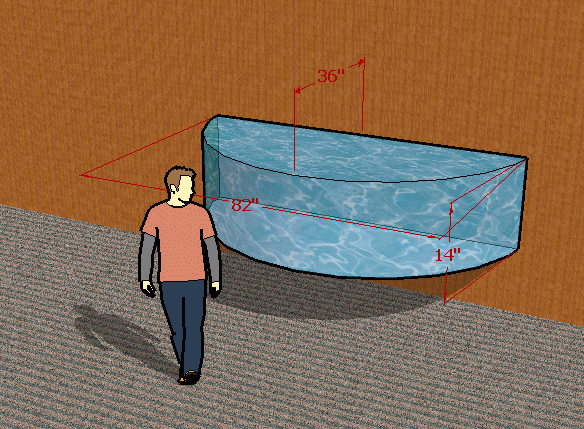
Because the length along the wall is more than twice the distance from the wall to the front, you don't actually have a full semicircle, in which case the calculation would be easier. Instead, this is a chord of a circle with an unknown radius.

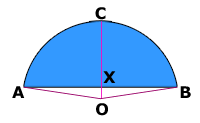Here is a top view.

The pink lines indicate radii from the three points on the tank to the implied center of the circle at point O. I've also labelled the other interesting spots we'll need to refer to.

The area in blue is a circular segment. The area of the circular segment is easiest to obtain by subtracting the area of the isoceles triangle OBA from the circular sector (pie slice) OBA. The volume of the tank is just the depth (14") times this blue area.

The area of a circular sector is ½r²θ where θ is the angle AOB in radian measure and r is the length of any of the pink radii. The area of the isoceles triangle is ½(AB)(OX). But (OX) is just the radius r minus the length CX, which we know is 36 inches and AB is 6' 10" which is 82 inches. So the area of OBA = ½(82)(r - 36). Thus the volume of the tank is V = (14) [ ½r²θ - ½(82)(r - 36) ] which reduces to

V = 7 [ r²θ - 82r + 36(82) ] .

So we need to find r and θ. Let's draw a more detailed diagram.

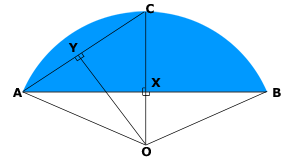Since OC bisects AOB, and OY bisects AOC, then we know that YOC = ¼θ. Also, since CX bisects AB, we know the length AX = ½(82) = 41 inches.

This means we know the length of two sides of AXC, so we can find AC by using Pythagorus:

     AC² = 41² + 36²
     AC = 54.58 inches.

Since OY bisects AC, then YC = ½(54.58) = 27.26 inches.

Also, since we know two sides of AXC, we can find the measure of XCA:

XCA = tan^-1 (41/36) = 0.850 radians.

And in OCY, we have C, so O = (π/2) - C = 0.72055 radians, so θ = 4(0.72055) = 2.8822 radians.

As well, r = CO = YC / (cos XCA) = (27.26) / cos (0.850) = 41.3 inches.

So we can put these values of r and θ into our equation for the volume:

V = 7 [ (41.3)²(2.8822) - 82(41.3) + 36(82) ] = 30652 cubic inches.

I see you are writing from Jamaica and I am uncertain whether Jamaicans use liters, US gallons or UK gallons for measuring water volume. Respectively, their conversion factors give:

V = 502 liters or 132.6 US gallons or 110.4 UK gallons.

Stephen La Rocque.>