Hi Charles.

Penny and I aren't familiar with your use of the term "vertical angle", but we think you are referring to half the opening angle of the cone. The opening angle is the angle at its top. In the diagram below, θ is half the opening angle and forms of of the angles of the right triangle I've drawn.

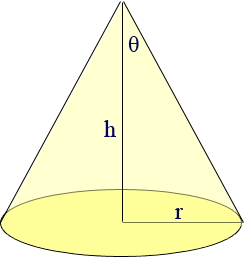Whatever you meant by the term vertical angle, it is clearly the angle that sets the cone's shape, so you can find θ from it. Thus, θ is a constant. Therefore, tan θ is a constant and since tan θ = r/h, we have

h = r tan θ,

which is a constant as well. Let k = tan θ. Then

h = r k.

The volume of a right circular cone with height h and radius r is:

So using our replacement for h, we have volume in terms of radius alone:

Now the rate of change of the volume is given as a constant: 9 m³ /s. Thus we know that at 10 seconds, 90 m³ of sand has piled up. What is the radius of this?

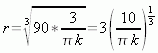
Now when we differentiate with respect to time we get this:

Remember that r in this context is the r value after 10 seconds. Solving for dr/dt we get the rate of change of the radius, which is what the question is asking for:

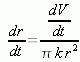
Now let us substitute our expression for r with the value of r after 10 seconds:

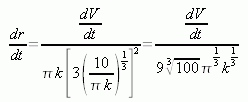
We are given that dV/dt is 9 m³/s, so let's simplify this:

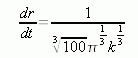
But here we have to stop, because we are unsure of the value of k due to the confusion over which angle you mean. If we proceed by assuming that the value θ that we identified in the diagram is in fact the angle you say is 60°, then

So when we substitute this in, we have:

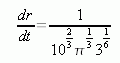
which is in meters per second. You'd multiply by 60 for meters per minute. This would give about 7.3 meters per minute. Using your formula, you'd get 1.56 meters per minute. We cannot reconcile your formula with ours, I'm afraid.

Stephen and Penny.