Hi Chetna. If I read your question correctly, then this diagram applies:

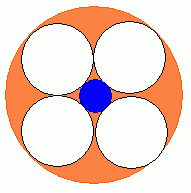
The radius of the orange circle is 10 cm. The white circles are congruent and tangent to the orange circle, each other and the blue circle. We want to know the radius of the blue circle.

Let's examine more closely, with some extra radii marked out:

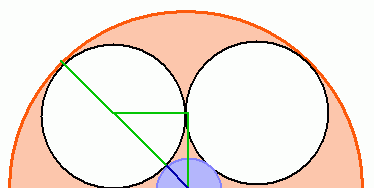
The green segments mark radii of the white circle and the blue segment is the radius of the blue circle.

Clearly two greens plus a blue is the radius of the orange circle, which is 10 cm.

Now let's look at this with just the bare essentials and give variable names to the lengths:

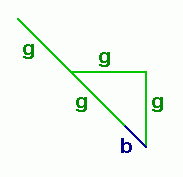
Clearly, we have an isoceles right triangle here. So using Pythagorus, we have
          2g² = (g+b)²

We also know from that the orange radius is 10 cm, so
          10 = 2g + b.

This means we have two equations in two unknowns, which you can solve in any of the usual ways.

Hope this helps,
Stephen La Rocque.

Chetna wrote back:

dear stephen.   i was not very satisfied with the answer. 
can you help me solce the two equations formed . 
as far as i can see, one is quadratic and the othe is simple.  thanks

Sorry to hear you are still having trouble, Chetna.

The easiest way to solve this is with substitution. Solve the second equation for b, then substitute into the first equation:

Solve for b:

10 = 2g + b therefore
b = 10 - 2g.

Now substitute:

2g² = (g + b)² therefore
2g² = (g + (10 - 2g) )².

Now you have just one unknown. Solve this last equation for g. When you have that, put it into the simple equation to find b.

Stephen.