| |||
| Math Central | Quandaries & Queries |
|
A coffee filter for a new coffee maker is to be designed using a conical filter. The filter is to be made from a circle of radius 10cm with a sector cut from it such that the volume of coffee held in the filter is maximised. Determine the dimensions of the filter such that the volume is maximised. This question is usually done by excel, with a formula of which I have an example of from another question. (=23*A2-2*A2^2) However, the only way I can think of answering this question is when I have the height (or slant height so to figure the height) but I'm pretty sure that more than the ratio is needed.... Can you figure out the maximised measurements some other way? I'm in need of desparate help. Cheers. |
Hi Christina.
The volume of a cone is given by the formula:
![]()
where r is the radius of the mouth of the cone, h is the vertical height and v is the volume. For a right circular cone, we could further label the slant length R on this diagram:
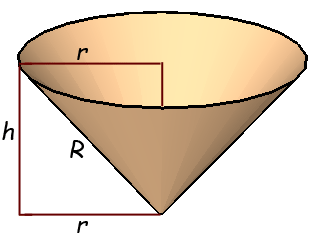
You will see the right triangle created. So we can apply Pythagorus' Theorem:
![]()
and solve for r2 :
![]()
Then we can replace the r2 in the volume formula with this expression:
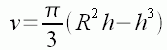
So by using a little calculus, we can find the height that maximizes the volume. First we take the derivative of both sides with respect to h (remember that R is a constant):
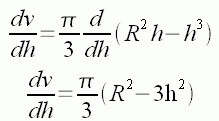
We know that when the derivative dv/dh is zero, we are at a critical point, which in this situation must be the point where the volume is maximized, so we set dv/dh to zero and solve for h:
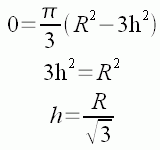
So now we know what value we want for h. Now we can find r from R and h:
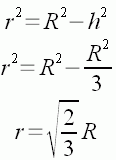
Now for the pattern of the coffee filter itself. The general flat pattern for a right circulator cone, like this coffee filter is:

We already know that the radius of the filter is 10 cm. We need to know how large a sector to cut from it.
But since we calculated the value of r that corresponds to the largest volume cone, we know that the outside circumference (excluding the missing portion) is the circumference of the mouth of the filter.
At this point we had an error. Stephen used the expression for the area of a circle rather than the circumference. In October 2009 Kerstin, a teacher, pointed out the error and sent this correction.
Using formula for circumference of a circle and letting x be the portion of the circumference to be cut out
2 × π × R - x = 2 × π × r = 2 × π × √(2/3) × R
x = 2 × π × R (1 - √(2/3)).
The angle of the slice to be cut out is alpha = x / R = 2 × π × (1 - √(2/3)) = 1.15 radians, which is about 66 degrees.
Stephen and Kerstin
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.