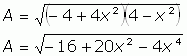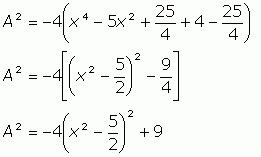Hi Claire.

This formula will be our starting point for your question:

For your triangle, you have sides of length 4, x and 3x, so:

and therefore:

.

Now if we multiply this out, we get:

This looks awful, but since the largest value of A will also lead to the largest value of A², why don't we just square both sides? I'll also factor out a -4.

If you look carefully at what is inside the parentheses, you can see that this is a quadratic in x². What that means is that we can think of y = x², so we have y² - 5y + 4. That's just a normal quadratic. So we can "complete the square" next.

Now look carefully at this equation. Because of the factor of -4, whatever is inside the parentheses is going to reduce A². Since we want the maximum value of A², we want the value inside the parentheses to be zero. You can easily work out the value of x that makes this so, but that isn't actually necessary in order to answer the question you've been asked. Simply, we know that inside the parentheses, the value can be zero, so we can ignore the first term entirely. Thus,

A² = 9, so A = 3.

The maximum area is 3 square units.

Hope this helps you,
Stephen La Rocque and Harley Weston.