Hi Cliff.

I was pretty sure we've already done questions like this, but is how to figure it out:

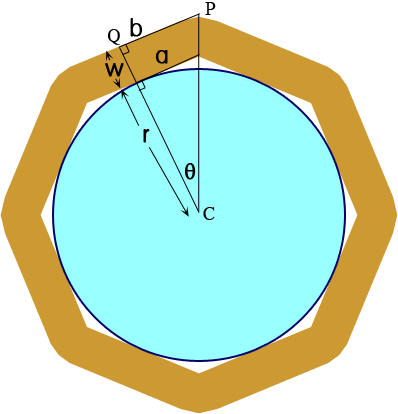
The radius of the pool (half the diameter) is r.

The width of the deck is w.

The rest we will calculate.

Now you can see that we are dealing with right triangles, so we can use simply trigonometry to solve the rest of the dimensions.

First consider what angle θ must be. How many identical triangles are there around the whole circle? There are 2 per side of the octagon, so there are 16 in all. How many degrees are there in a full circle? 360. So θ = 360°/16 = 22.5°. And this is what angle your cuts would be made at as well.

Now we know r (in your case it is 17 ft / 2), so a = r tan θ and b = (r + w) tan θ.

Remember that a is half the inside length of each octagon's side and b is half the outside length.

So each piece of the octagon has an inside length of 2r tan 22.5° and an outside length of 2(r + w) tan 22.5°.

In your case you have a pool that is 17 ft in diameter, so r = 8.5 ft. Let's say you want a deck that is 2.5 feet wide (that is, w = 2.5), then you need eight sides whose

• inside length = 2(8.5 ft) tan 22.5° = 7.04 ft and
• outside length = 2(8.5 + 2.5) tan 22.5° = 9.11 ft

The angle QCP, labeled θ in the diagram, measures 22.5° and hence angle CPQ measures 90° - 22.5° = 67.5°. Thus, in cutting the boards to make the octagon, set the saw angle at 67.5°.

Hope this helps,
Stephen La Rocque.