Hi Courtney.

I'll show you how to solve this for a regular heptagon (7-sided) and you can use this method to solve your octagon problem the same way.

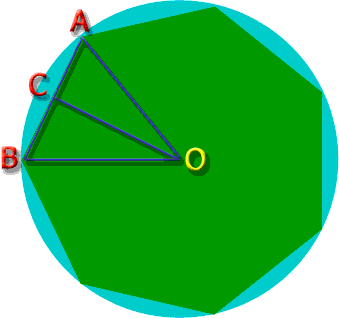
The radius of this circle is R. That is the distance AO and AB, since they are both radii. That makes triangle AOB an isoceles triangle.

As an isoceles triangle, A=B. Let spot C be chosen by drawing a bisector of angle AOB. So AOC = BOC. But that means that BCO = ACO, because two triangles who have two matching angles have all matching angles. This means ACO is similar to BCO. Since they share a common side, then they are actually congruent. This means that BC = AC, which is a very important fact we'll use.

What is the measure of angle AOC?

It is half the size of AOB of course, but how big is that?

Notice that we arbitrarily chose one of the seven congruent triangles that we could have drawn joining the center of the figure to one of the sides of the heptagon. So if we were to add up all the angles of all seven triangles at the center, we would have a full circle: 360°.

Since they are congruent, each angle is the same: 360°/7 = 51.43°. So angle AOC is half that: 25.72°.

Notice also that since A-C-B is colinear (lies on a line), then angle BCO + ACO = 180°. But since these angles are the same because of congruent triangles, then ACO must be 90°.

So ACO is a right triangle and you know the length of the hypotenuse (R) and the measure of the angles, so you can calculate any side length. In this case, we want length AC, so we use the sin function.

sin 25.72° = AC / AO

AC = AO sin 25.72°

Since AB = 2 AC as we showed earlier, AB = 2 AO sin 25.72°.

And since there are seven such triangles that are congruent, the perimeter of the heptagon is 7 AB.

and so the perimeter = 7 x 2 AO sin 25.72° = 14 R sin 25.72°.

For a radius of R = 12 cm, the perimeter would be:

14 (12 cm) sin 25.72° = 72.9 cm.

Now you try it with the octagon. Its perimeter should be more than the 12cm heptagon here.
Stephen La Rocque.