Hi Cristin.

No, one angle is insufficient. We need as many angles and/or diagonal lengths as required to keep the shape from "hinging". We have a short video demonstration of this here.

You did, however send us a reasonable diagram, so I can make an estimate based on the diagram, although I should stress that this is only an estimate.

Finding the area of a lot using a sketch without angle measurements

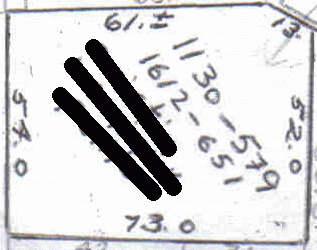
Step 1: Print it very carefully

Many printers do not have perfectly square pixels/dots so you have to check that the aspect ratio is correct when you print a diagram you'll use to infer accurate distances. One way to do this is to calculate the scaling factor of vertical lines and compare that with horizontal lines. The scaling factors should (or must be made to) match.

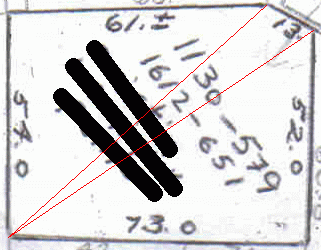
Step 2: Draw diagonal lines such that you've divided the shape into triangles.

This allows us to calculate the area of all the triangles individually and add them together. When you divide a shape into many smaller shapes, the total area remains unchanged. Here is the result.

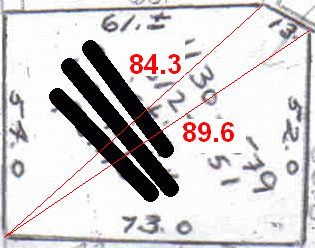
Step 3: Accurately measure the lengths of the diagonals.

You need to use the scaling factor you determined in step 1 for this. In your case, Cristin, since you told us that the 52 and 73 sides meet in a right angle, I was able to use the Pythagorean formula to calculate the lower red line length.

Step 4: Use Heron's Formula to calculate the area of each triangle.

The area of any triangle can be calculated if you know the lengths of all three sides. This is Heron's Formula. The side lengths are a, b, and c and the value S is the "semi-perimeter" of the triangle, which equals (a+b+c)/2, of course:

So for the top left triangle, a = 54, b = 61 and c = 84.3. Thus S = 99.65. So when I punch that into the equation, I get an area of 1642.8 square feet.

I'll leave it to you to calculate the other two triangular areas (you didn't expect me to do all the work, did you? )

Step 5: Add them up!

Now you have the total area of your lot.

Hope this helps,
Stephen La Rocque.