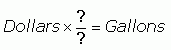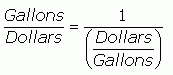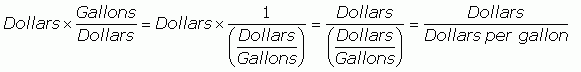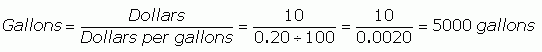Hi Cynthia.

I think I understand the question, but I'll re-phrase it. You let me know if I'm off.

Water costs $0.20 per gallon. If you bought $10 worth of water and divided it equally among 3 people, how many gallons would each one have?

There are two steps to the problem: First you need to find out how much water $10 buys, then you need to divide that by three.

Here's how I solve this kind of problem.

We need to convert units from Dollars to Gallons. Units (like "dollars", "gallons", "widgets" or "thingamajigs") work just like numbers in equations. So you can use them to determine the formula to use. Fractions are usually really useful in conversion questions. That is, fractions with words rather than numbers (they come later). We are looking for a fraction that is a "conversion factor".

I have DOLLARS. I want GALLONS. What fraction makes the equation work so that it will equal?

I know that with fractions, something on the bottom that is the same as something on the top will "cancel". So this should work:

But I don't have anything in the question representing Gallons divided by Dollars, or do I? Remember that when a fraction is in the denominator, then that is the same as when the reciprocal is multiplied? It is the same going backwards:

So I can replace the Gallons divided by Dollars with this other expression (if they are equal I can always replace one with the other).

You see how Dollars divided by Gallons means the same thing as Dollars per gallon? And that's something I know (well, I know dollars per 100 gallons, so I just divide it). So now I substitute in the actual numbers into this expression:

Now I know how many gallons of water the trio bought. So I can divide by three to find the final answer.

Even though I went through this problem with a lot more detail than you were probably expecting, Cynthia, I think if you look closely at how I used the units to figure out how to solve it, you will be able to solve very many similar problems in the years to come.

Cheers,
Stephen La Rocque.