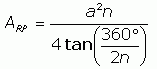Hi Dana.

We often get questions about regular polygons (that is a polygon which has all equal angles and sides) and calculating their areas.

Whatever the number of sides you have in the polygon, you can find the area of the polygon from the side length by dividing the shape into isosceles triangles with a vertex at the center of the shape.

I'll demonstrate with an heptagon:

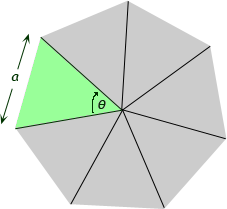
The side length is a. You can see that every triangle must be congruent to the one I did in green. So the area of the heptagon is seven times the area of one triangle.

Since all the triangles are congruent, the angle at the center is also the same all the way around. A full circle makes 360°, so the angle θ must be 360° / 7.

The area of an isosceles triangle which has a base length of a and the vertex angle of θ is just

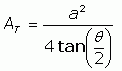
So the area of the heptagon is seven times this, with the value of θ = 360° / 7:

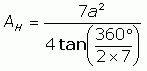
And in general we can write the formula like this:

So Dana, for a tetradecagon with 8 ft sides, use n = 14 and a = 8 in the equation above to find the square footage.

Hope this helps,
Stephen La Rocque.