6 numbers from a set of 12

Math Central

Quandaries & Queries

Question from Darren:

there are 12 numbers (1-2-3-4-5-6-7-8-9-10-11-12)
how many times can i pick 6 differnt numbers?
thanks Daren

Hi Darren.

How many different groups of 6 people can you choose from 12 people? Same question.

We are looking at groups, so this is a "combinations" question.

In maths, we would there are a few different notations that are used. You may be familiar with any of these, which all mean the same thing:

nCk

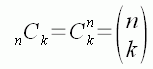
n is the total number of items from which you are choosing and k is the number of items you are choosing. So for your question, you need to calculate ₁₂C₆.

The formula for such combinations uses factorials (designated with an exclamation point ! ). Here is the formula:

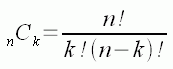
$C_{k} lsub{n} = {n!} over {k!(n-k)! }$

So the answer to your question is the value:

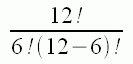
{12!} over {6!(12-6)! }

Hope this helps,
Stephen La Rocque.

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.