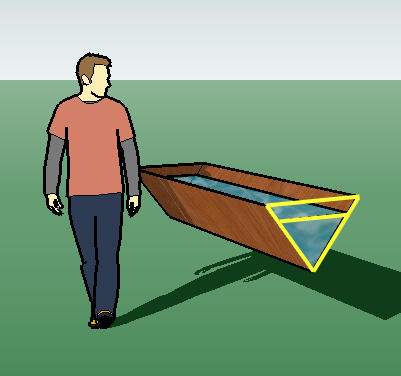
Hi David.

I get the same answer for part (i) as you did.

Between part (i) and part (ii), the shape doesn't really change, just the height of the triangle (depth of the water). This means we have similar triangles (see them in yellow on the left).

Since the length of the trough is constant, we can ignore it and just think about the ratio of the area of the large triangle to the inner triangle. That should be the same as the ratio of the volumes.

The base and depth (height) of the large triangle is 0.6m and 0.4m (from Pythagorus). So the area of the large triangle is 0.24 m². Since the volume ratio is the same as the area ratio, that means the area of the smaller triangle must be 0.12 m².

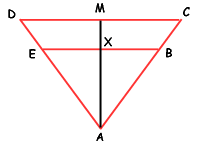The triangles are similar triangles. This means that the ratio between their parts is the same for any pair. So DC / EB = k, where k is this common ratio (we aren't sure of the value of k yet). Also, you should be able to reason that MA / XA = k. But we can therefore multiply the left sides together and the right sides together:

(DC / EB) (MA / XA) = k².

But if we multiply by (½ / ½) on the left side and move the parentheses around a bit, we have this:

(½ DC × MA) / ( ½ EB × XA ) = k².

But aren't those just the areas (one half base times height) of the large and small triangles ? That means that we can replace them with the volumes:

(240 litres) / (120 litres) = k².

Now you can calculate k and then divide MA (which we noted earlier is 0.4 m) by k to find the length XA. This is the depth of the water when the volume of water is half the volume of the trough.

Hope this helps you,
Stephen.