Hi Denise.

I'll show you how this is done using different figures:

P(x) = R(x) - C(x)
R(x) = 31x - 2
C(x) = 0.5x² - x + 10

First, make P(x) depend on x without reference to R(x) and C(x).

P(x) = (31x - 2) - (.5x² - x + 10)
P(x) = -0.5x² + 32x - 12

The maximum value of P(x) is at a "critical point", so that means

^dP /_dx = 0

So when we take the derivative of P, we get this:

^dP /_dx = ^d /_dx (-0.5x² + 32x - 12)

0 = -x + 32
x = 32

Since this is the only critical point, this is our answer.

So with my numbers, the maximum profit occurs when the number of units
(x) is 32 and that maximum profit is P(32) = -0.5(32)² + 32(32) - 12 = £ 500.

I've drawn a graph of P(x) so you can see what is happening:

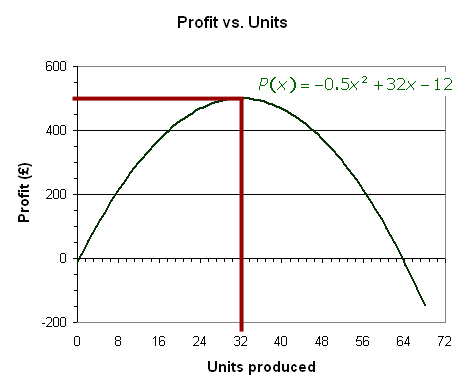
Now you try this method with your figures.
Stephen La Rocque.