There seems to be a basic confusion just behind the question. For most of mathematics (including classifying quadrilaterals) the definitions are inclusive.

So a quadrilateral with no parallel sides might be a trapezium, but so would any quadrilateral be, even with parallel sides, I think. It is unusual to use trapezium in this context, in North America. (We know this is different in England!)

A kite is a quadrilateral with one mirror (across a diagonal) at least. This includes the possibility of some parallel sides, it includes a rhombus, which has two mirrors, and two pairs of parallel sides. It even includes a square! Similarly, a square is a rhombus, as well as a rectangle.

There is a way to classify quadrilaterals based on the symmetries, which reinforces the symmetry concepts, and keeps the inclusive definitions. Here is a picture of this.

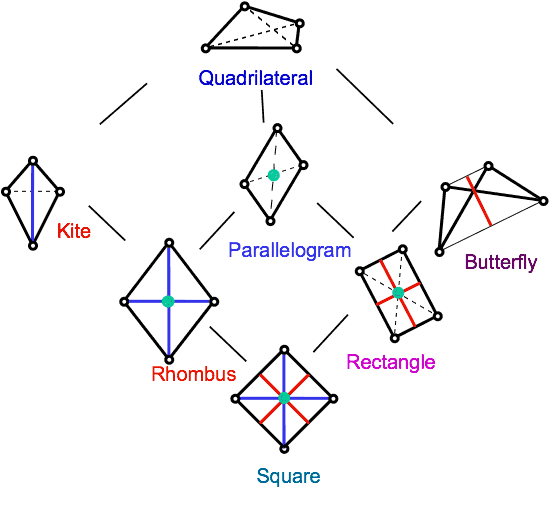
The green dots are centers of rotation, the red lines are mirrors between midpoints of opposite sides, and the blue lines are mirrors between opposite vertices. Perhaps eccentrically, I have used the name butterfly to capture the objects named (in North America) isosceles trapezoids.

Walter Whiteley

Don,

The terms trapozoid and trapezium are confusing both because the North American and British definition differ and also because there are two common definitions of trapezoid in North America. One definition of a trapezoid is a quadrilateral plane figure having two parallel and two nonparallel sides the other that a trapezoid is a quadrilateral plane figure having two parallel sides. The second definition stisfies Walter's comment that "For most of mathematics (including classifying quadrilaterals) the definitions are inclusive."

Penny