George, we have three responses for you:

Hi George.

I've sketched the volumes involved below.

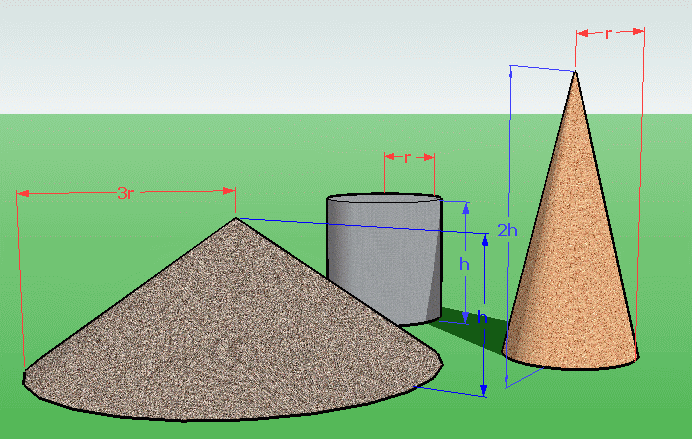
The formula for the volume of a cylinder is v = πr²h. The volume for a cone whose radius is R and whose height is H is V = ¹/₃πR²H.

A) Tall cone. The cone's height H is twice the height of the cylinder h, so H = 2h. And the radius of the two match, so R = r. Now you can substitute in:

V = ¹/₃πR²H

V = ¹/₃πr²(2h) = ²/₃πr²h = ²/₃(πr²h) = ²/₃v = ²/₃(1353 cm³)

B) Wide cone. Your turn, George. Follow the same idea.

Hope this helps,
Stephen La Rocque.

George,

Rather than a quick fix for these pieces, it helps to have a larger 'sense' of what is going on. With this 'sense' of how volume changes, each of these pieces will be simple enough. So here are some principles which should help.

(1) How does a cone relate a cylinder, circular or not? This is an old problem, studied back at least to the Greeks (Archimedes knew it, and even had something related to it engraved on his grave stone!).

The general principle is: for a fixed 'base' (any shape) and a fixed height, the cone (joining everything on the base to one point at that height) is 1/3 the volume of the cylinder of the same height.

The analogy is that, in the plane, the area of a triangle (one point joined to a 'base') is 1/2 the area of the rectangle of the same base and the same height. (Yes the 1/d is what dimension you are in. For four dimensions the analogous result would be 1/4 .... )

(2) How does volume of a 3-D object change if you freeze two of the dimensions (e.g. width and depth) and scale only one (the height). The basic principle is that the volume scales as the one dimension scales. So scaling height by 3 will scale volume by 3, etc. The example is just a simple box V= LxWxH. Scale one of these, say height, by k and the volume scales by k.

(3) When you scale two dimensions by k, then the volume scales by kk = k². (Just as the area of the base will scale by k²) . So the key is that scaling 'the radius' of a circular cone is scaling both width and depth by that scale factor.

(4) Although this problem did not ask it, the final step would be scaling all three dimensions at the same time by k, and therefore scaling the volume by k³.

Hope that helps.

Walter Whiteley
York University

Hi George.

Cones and cylinders are quite similar solids, each needing only two parameters to specify their dimensions: radius (distance from the central axis to the outer edge along the base) and height (length of the central axis). Usually these are denoted as "r" and "h", respectively.

The formula for the volume of a cylinder is

Volume = (Area of Base)*(height)

where the area of the base is the area of a circle of radius r, that is

Area of Base = pi*(r²) = pi*(r)*(r)

Thus the volume of a cylinder is

Volume = pi*(r²)*h

Similarly, the formula for volume of a cylinder is

Volume = (1/3)*pi*(r²)*h

That is, the volume of a cone is 1/3 the volume of a cylinder with the same radius and height. Now, you are given a volume for the cylinder, but neither the height nor the radius. You can write (for the cylinder)

1353 cm³ = pi*(r²)*h

A cone of the same r and h should have 1/3 this volume. But we want a cone with double the height, therefore

Volume of Cone = (1/3)*pi*(r²)*(2h) = (2/3)*pi*(r²)*h

Where I have re-written the formula to include the 2 and 1/3 in a single fraction. Notice that the part immediately after the (2/3) is exactly the same as the formula for the cylinder, which we know the volume of. Therefore we can substitute 1353 cm³ for the pi*(r²)*h. Doing so will give us the answer to (A).

We can do the same thing for (B), but now we want to write

Volume of Cone = (1/3)*pi*((3r)²)*h

to get a cone with triple the radius but the same height. To rewrite this in a form that explicitly shows the volume of the cylinder, we'll need to square the 3 along with the r...

Volume of Cone = (1/3)*pi*((3r)²)*h = (1/3)*pi*((3²)*(r²))*h = (1/3)*pi*(9r²)*h = 3*pi*(r²)*h

Now you can replace the pi*(r²)*h with the volume of the cylinder provided, and calculate your answer!

Hope this helps.
Gabe.