Hi Henry.

You are describing a circular segment whose area is (¹ /₃ )r² , but I suspect you already know that.

The area of a circular segment can be deduced from the area of the circular sector and the area of the isosceles triangle within the circular sector. This diagram helps explain things:

	minus		equals
A=½r2		A=½r2sin		A=½r2(-sin)

Thus, you want to solve (¹ /₃ )r² = ½r²(-sin), which simplifies to 3 - 3sin - 2 = 0. Note that the angle is the central angle measured in radians.

This equation is not easy to solve. In fact, the easiest approach is to solve it numerically (that is, to find a close approximation).

Using a spreadsheet package, I calculated an approximation of f() = 3 - 3sin - 2.

Clearly, must be between zero and radians, so using those as the initial boundaries, I quickly divided the range of possible values of in half and zeroed in on the approximate value of that answers your question.

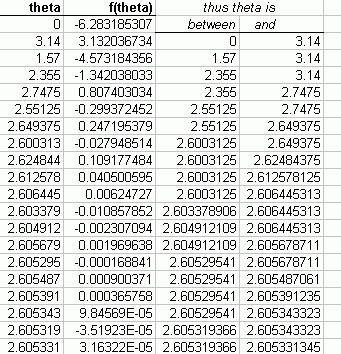
So 2.6053 radians. Thus, a circular segment subtended by an angle of 2.6053 radians has an area of one third of the area of the circle itself.

The length of the chord can be calculated given the radius r and this angle using simple triangle geometry:

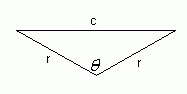implies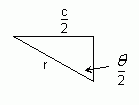

so sin( / 2) = (c / 2) / r.

Hope this helps,
Stephen La Rocque.