Hi James.

Here is a diagram I drew of your problem. I've also drawn the radius of the outer circle as R and the radius of the inner circle as r. Remember that at the point of tangency, the tangent line is perpendicular to the radius of a circle, so this triangle is a right-angled triangle. As well, symmetry requires that the side of the right triangle be half of the chord length, so I've labelled it 7 cm.

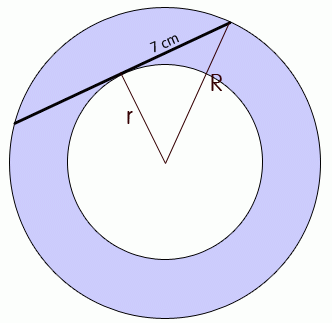
The area of the outer circle is πR² .
The area of the inner circle is πr² .
Therefore the area of the shaded region is the difference of the two:

     A = π(R² - r²)

Since that is a right-triangle, Pythagorus applies, so

     R² = 7² + r²
     R² - r² = 7²

Thus,

     A = π(7²)