Hi Jenny.

I think you are trying to write:

1. θ = 6π/7
2. θ = 3.3

Generally, when angles measurements have a π in them, that is a good indication that the question means for you to work in radians, rather than degrees. Remember that 2π radians = one full circle = 360°.

So start by drawing a unit circle and figure out where the angle θ appears. I've drawn an example where θ is about 2 radians. You can determine which quadrant it is in by looking at the angle measure and seeing if it is between 0 and π/2 radians (Quadrant 1), π/2 and π radians (Quadrant 2), etc. I know that 2 radians is in quadrant 2 this way, so I've drawn it as a blue radius. The angle θ is the angle from the positive x axis counterclockwise to this radius.

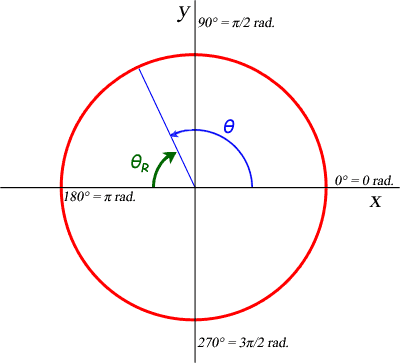
The reference angle associated with any angle is the positive value of the angle between the radius and the x axis (either side: positive or negative). In my drawing, I've noted the reference angle for θ as θ_R and shown it in green. To calculate the value of my reference angle, I just subtract it from π, since I am referring to the negative x axis. So in my case, θ = 2 rad. and θ_R = π - 2 = 1.14 rad.

Cheers,
Stephen La Rocque.