 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
Question from Jerry: Points A and C lie on the circumference of a circle. B is a point inside the circle. When produced, AB and CB meet the circumference at points E and D respectively. Prove that AB = CB, then EB = BD. |
Hi Jerry. I can get you started on the proof. Start by connecting C to A and E to D.
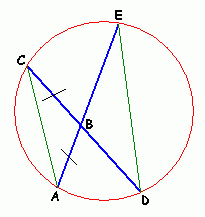
| Statement | Reason | |
| CB = AB | Given. | |
m ABC = mEBD |
Opposite angles of intersecting lines are congruent. | |
| mDCA = mDEA |
All inscribed angles subtending the same arc (in this case arc AD) are equal. | |
 ABC is similar to EBD |
Angle-Angle similarity. | |
| ... |
Hope this helps,
Stephen La Rocque.
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.