 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
Question from Jonathan, a student: My calculus teacher gave our class this question and said he was not able to find the answer in all his years of teaching. Somehow I think there is some information missing but maybe not. Any ways the question is, "A certain Clock has a minute hand with a length of 4 inches long and an hour hand with a length of 3 inches long. How fast is the distance between tips of these hands changing at 9:00?" If someone is able top get the answer to this question, AWESOME JOB! If not, thanks anyways. |
Hi Jonathan.
It seems to me that this problem doesn't involve calculus, but rather just vectors. Allow me to explain.
The angular velocity of the ends of each hand are constant, so the tangential velocities are as well. To convert, we use the formula v = rω where v is the tangential (linear) velocity and ω is the angular velocity.
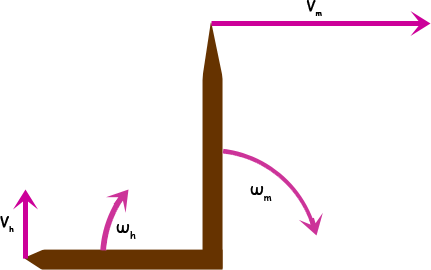
Thus the tangential velocities are
vh = 3 inches × ( 2π radians / 60 min) in an upwards direction and
vm = 4 inches × ( 2π radians / 1 min) in an rightwards direction.
The change in distance is simply the difference of these two vectors. If I reverse the minute vector so that I can add rather than subtracting vectors, I find a simple right triangle to solve:
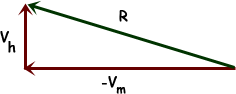
Since you are just interested in the speed the distance is changing, you just need to find the magnitude of R, which Pythagorus can help you with.
Hope this helps,
Stephen La Rocque.
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.