Two-column proof for a circle geometry problem

HOME

Math Central

Quandaries & Queries

Question from kendra, a student:

i have to prove that tangents to a circle at the endpoints of a diatmeter are parallel by stating whats given, whats to prove and a plane, then write a two column proof i dont understand this

Hi Kendra.

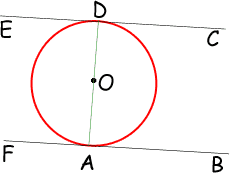
I would start with a diagram something like the one below and label it with letters so I could refer to it in the proof:

Now you can state what is given:

Line FB is tangent to circle O at A
Line CE is tangent to circle O at D
Line AD is a diameter of circle O

And what you are to prove:

Line FB is parallel to line CE

And formulate a plan for the proof:

Show why OA is perpendicular to FB and OD is perpendicular to CE
Show why angle EDA is congruent to angle BAD
Show why angle EDA and angle BAD are alternate interior angles of the transversal AD across lines FB and CE.
Conclude that this makes FB and CE parallel.

A two-column proof is one where the left hand side gives the mathematical statements based on given information or on information from earlier steps in the proof and the right hand side contains the reason why this step makes sense. The reasons are generally either "Given", some kind of definition of terms, known theorems you can apply, or logical deductions that follow from the earlier steps. The proof ends with a statement of what you were trying to prove of course:

Statement	Reason
Line FB is tangent to circle O at A Line CE is tangent to circle O at D Line AD is a diameter of circle O	Given.
FB is perpendicular to the radius AO CE is perpendicular to the radius DO	Definition of tangent.
angle EDA is a 90 degree angle angle BAD is a 90 degree angle	Definition of perpendicular.
angle EDA is congruent to angle BAD	Definition of congruent.
AD is a transversal of the lines FB and CE	It crosses (intersects with) them both.
angle EDA and BAD are alternate interior angles	Definition of alternate interior angles.
line FB is parallel to line CE	Known theorem: If any two lines are cut by a transversal such that alternate interior angles are congruent, then the two lines are parallel.

And that's how you do a geometric two-column proof.

Cheers,
Stephen La Rocque.

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.