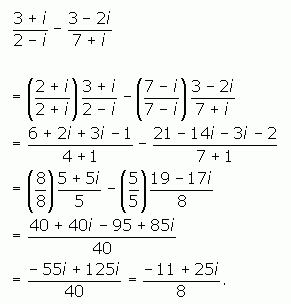| |||
| Math Central | Quandaries & Queries |
|
Question from Krys, a student: How do I simplify completely? ((4+i ) / (3+i )) - ((2-i ) / (5-i )) |
Hi Krys.
The important principle is to use the difference of squares principle to your advantage. The square of i is negative one, of course, so (a + bi)(a - bi) = a2 + b2. See how the imaginary part disappears?
Although I cannot solve your entire problem for you, I'll solve one that is identical in form to yours to show you how I use this principle.
Hope this helps,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.