 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
A beam on a lighthouse 2000 metres away from the nearest point P on a straight shoreline revolves at the rate of 10 pie radians per minute. How fast is the beam of the light moving along the shoreline when it is 500 metres from P? |
Hi Lisa.
I've drawn the situation below.
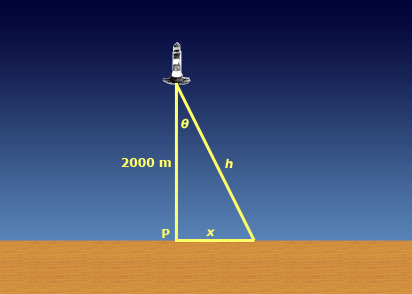What you are trying to find is dx/dt when x = 500 m. You are given
d
/dt = 10
radians/minute.
Recall that tan = x / 2000, so
x = 2000 tan
Take the derivative of both sides with respect to time and you get:
dx/dt = 2000 d/dt (tan )
Can you use the chain rule and solve the rest of the problem? You'll need to substitute the appropriate value of when x = 500, which you can find by using the Pythagorean theorem.
Hope this helps,
Stephen La Rocque.
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.