Hi Lori. I hope this diagram fits your description:

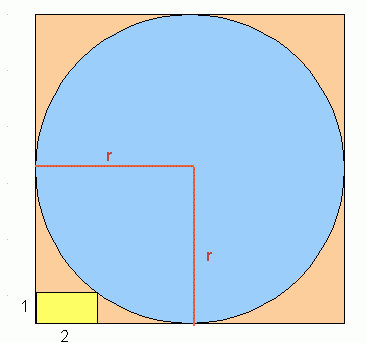
You want to find r, the radius of the circle.

The equation of a circle is:

(x - h)² + (y - k)² = r²

where (h, k) is the center of the circle. So if we can determine the equation of the circle, we can determine its radius.

Let's start by putting the origin in the bottom left-hand corner. Then the center is (r, r), so we have

(x - r)² + (y - r)² = r²

What's the location of the corner of the yellow rectangle where it touches the circle? It is (2, 1).

So we can substitute that value of (x, y) into the circle's equation:

(2 - r)² + (1 - r)² = r²

Lori, can you finish the problem from here?

Hope this helps,
Stephen La Rocque.

Hi Lori,

When I read your question I didn't understand it but Sue did. When I read Sue's solution I saw another way to approach it so I took her diagram, added two lines and labeled three points.

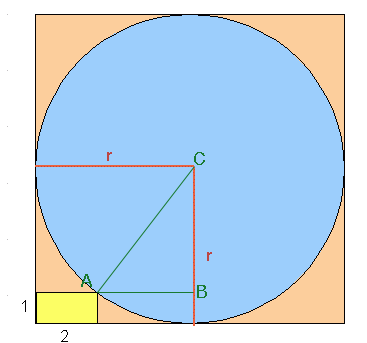The length of CA is r. What is the length of AB? What is the length of BC? What does Pythagoras' theorem tell you? Penny

Lori wrote back.

This question is for sue and penny. First Sue, I put ones in for the place
of the r's and got the answer to be 1, but that doesnt seem right. Am
I even doing this right?

Next Penny, I know that the Pythagoreum Theorem tell me a² + b² = c² but
I am not sure at all what to do after this.

Thanks for everything

Hi Lori. Yes, one of the solutions to the equation is 1, but that doesn't fit the diagram. However, it does fit most of the
mathematical description. Take a look at this diagram below.

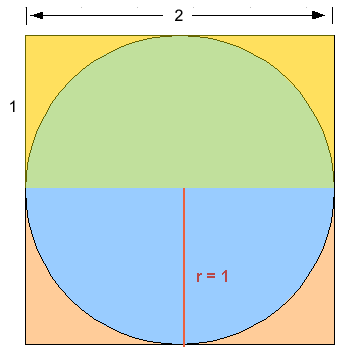
Can you see that this fits the description?
- A circle is inscribed in a square? yes
- A small rectangle with a 2 ft. top and a 1ft side at the left in the square touching the corner of the circle? yes, the rectangle is in the upper left corner of the square and the corner of it touches the circle.

That's why the value 1 works. However, for the diagram as I've drawn it earlier, there must be another solution, and there is. Does r = 5 work?

Stephen La Rocque>

Lori.

In my diagram the triangle CAB is a right triangle and hence you can apply Pythagoras' theorem.

If the length of the side AB is a, the length ofthe side BC is b and te length of the side CA (the hypotenuse) is c then
a² + b² = c². If you use the diagram to find the lengths of AB and BC then Pythagoras' theorem gives you an equation that is equivelent to the equation Sue found, (2 - r)² + (1 - r)² = r² .

Penny