Hi Maria.

The area of a circle is based on its radius - I am sure you know the formula for that, so I will solve a parallel problem for you to show you how to go about solving your own question.

My problem: One green square is inside a yellow square as shown below.

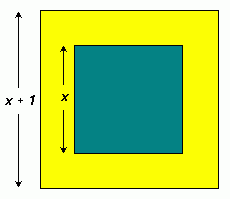The area of the green square is one third the area of the yellow border. The side length of the yellow square is 1 unit more than the side length of the green square.

What is the side length of each square?

Solution:

Let Y = area of the yellow square and G = area of the green square.

Then Y - G = the area of the yellow border.

Since the area of a square is just the square of the side length, we know
Y = (x + 1)² and G = x².

But we are also told that the area of the green square (G) is one third the area of the yellow border (Y-G), so:

G = (¹ /₃ )(Y-G), hence

x² = (¹ /₃ ) ( (x + 1)² - x² )

3x² = ( x² + 2x + 1 - x² )
3x² = 2x + 1
3x² - 2x - 1 = 0
(3x + 1)(x - 1) = 0

This gives two answers, but one of them is negative, which doesn't fit the idea of a side length, so we can ignore it. Therefore x = 1, so the green square has sides of 1 unit each, and the yellow square has sides of 2 (that's x + 1) units each.

In this case, I needed to solve a quadratic equation by factoring, but I could have used the quadratic formula if I couldn't easily factor it.

When you use this method for your concentric circles, you'll get the right answer to your question.

Hope this helps,
Stephen La Rocque.