Hi Mark.

I've rewritten your problem. Hopefully this is what you intended:

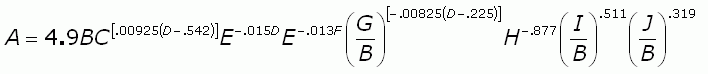
As I hope you can see, I only appears once in this expression. That means we can first multiply by the reciprocal of all the non-I stuff on the right. Whatever we do to one side of the equation we must do to the other. Taking the reciprocal of a number is the same as changing the sign on the exponent. For example, the reciprocal of 3 is 3^-1, which is one third. The reciprocal of x^-. 2 is therefore x^.2. We'll use this concept.

First multiply both sides by the reciprocal (negative exponent) of everything on the right side except the (I/B) term. This cancels all those terms on the right.

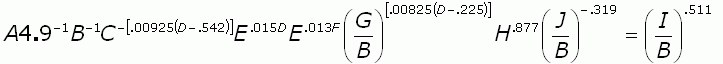
Now two more steps: when you divide, you are subtracting the exponents, so any denominators are just factors with the exponent sign changed. Break up the fractions therefore. To simplify the right side above, we want to multiply both sides by B^.511 . Also, I'll flip sides across the equal sign:

Now the first step in simplifying the right side is to group like terms (I mean those with the same base under the exponent). Multiplying two numbers in exponent form that have the same base is accomplished by adding the exponents together:

Finally, get rid of the exponent on the left side by taking each side to the power of the reciprocal of .511. Remember that when taking the exponent of a value in exponent form, you multiply the exponents. And since any number times its reciprocal is 1, this gets rid of the exponent on the left side, leaving just I.

I'll leave the rest to you. You just need to review the rules of working with exponents, Mark. Study those and such questions will come much more easily to you, even if they look really messy like this question.

Stephen La Rocque. >