What a marvelous find, Marleen!

I think they were building archways.

Let's say you need to know the distance across an arch 2m below the top (we call that 2 m line the sagitta):

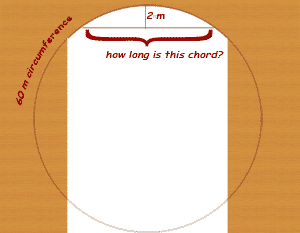
Babylonian Method:

Let's write this in using algebra, with C being the length of the circumference, x being the length of the chord and P being the perpendicular.

Thou double 2 and get 4

That's 2P.

Take 4 from 20, thou gettest 16

20 is C/3. So this is C/3 - 2P.

Square 16, thou gettest 256

That makes (C/3 - 2P)².

Take 256 from 400, thou gettest 144

400 is (C/3)². So we now have (C/3)² - (C/3 - 2P)².

Whence the square root of 144, 12 is the chord.

So they get x = sqrt( (C/3)² - (C/3 - 2P)² ). That's interesting. Let's compare that to what we get if we use modern mathematics. I'll draw another diagram:

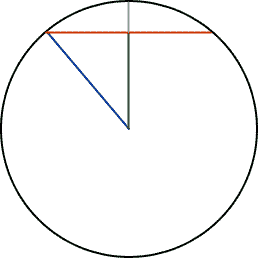Modern Method:

Now the radius is in blue and we know that the radius is the circumference divided by 2π: r = C/(2π). But the gray line's length is P, so the green vertical line (that's called the apothem) is r - P. That means its length is C/(2π) - P.

But we have a right triangle here, so the Pythagorean theorem applies. The length of the red chord is x, so the length of half the red chord (the length of the top of the triangle) is x/2.

Pythagorus tells us that

     (x/2)² = r² - (r - P)² = (C/(2π))² - (C/(2π) - P )².

If we multiply by 4 on both sides, we get:

     x² = (C/π)² - (C/(π) - 2P)².

Take the square root of both sides and we have:

     x = sqrt( (C/π)² - (C/π - 2P)² ).

Comparison:

Now we can take the square root of both sides and compare our answer to the Babylonians':

Modern day: x = sqrt( (C/π)² - (C/π - 2P)² ).

Babylonians: x = sqrt( (C/3)² - (C/3 - 2P)² ).

So their equation is identical to ours, except that they use a 3 in place of π. Not too bad: it's within 5% of the real value of π.

Thanks for the fun,
Stephen La Rocque.