| |||
| Math Central | Quandaries & Queries |
|
Question from Matthew, a student: I have what I like to think of as a rather interesting question that I can't explain confidently for the life of me. If we take a circle with a radius of 1 and we calculate the circumference, we can use 2 pi R. Doing this calculation results in a circumference of 6.28318530717~ which goes on forever. However, if you were to take a that same circle in the real world, say with radius 1cm and wrap a string around it, and then measure the string, you don't get 6.28~, you get something like 6.2, a much more finite distance. The length of the string is not an irrational number, like the math claims it to be. Naturally this occurs because pi is an irrational number, but why is it? My only guess is that our current estimation of pi is not actually correct to "true pi", but its just really really close. If however this is the case, why hasn't the "true pi" been discovered? Is anyone actually working on that problem and what kind of methods are used for such a thing? Any insight that can help me get a better understanding of this problem would be much appreciated. |
Matthew, we have two responses for you:
Matthew,
If you measure the time two sprinters take to run 100 meters, the answer you will get depends on the instrument you take:
- With your wrist watch you might say the winner took 10 seconds and the loser 11 seconds.
- With a good stopwatch you might say the winner took 10.2 seconds and the loser 10.9 seconds.
- With a video camera you might say the winner took 10.218 seconds and the loser 10.874 seconds.
- With even better instruments you might even say that the winner took 10.217734 seconds and the looser 10.874037 seconds.
- And so on.
So I would say that the ``real time'' that the sprinters take, if such a thing exists, is an irrational number.
It is the same thing with pi: If I measure the circumference/diameter of a small coin with a string, I am happy to get 3. But if I take a larger circle and use better instruments, I get 3.14. With even larger circles and even better instruments, I would get even more decimals correct. And so on.
But because pi is a mathematical concept (ratio of circumference to diameter on an idealised circle) rather than a physical event (a race), it is possible to compute it mathematically rather than physically. On this University of St. Andrews web page we read that after centuries of calculations with polygons,
John Machin used the formula π/4 = 4 arctan(1/5) - arctan(1/129) and James Gregory's series for arctan(x) [to get 100 decimals of pi.]
Lambert proved that pi was irrational in 1761.
Claude Tardiff.
Hi Matthew.
How are you measuring the length of your string and the radius of your circle?
You are using a device that only has a certain amount of precision. A ruler might measure 0.05 cm at best, other devices can get much more precise, but no device can get the uncertainty below about 10-33 cm (and no such device is possible!). So there is in fact a "rounding off" implicit in your measurements.
Pi is a number which is irrational, and so numeric representation of it will necessarily be an approximation (3.14, for example, or 22/7 or 3.1415926535897932384626433832795029). However, we don't just have "approximations" or "estimates" of pi. We know its value precisely, we just can't express it in decimal or fraction form, because then it would be rational (by definition).
Some valid and absolutely precise expressions of Pi:
- The ratio of the circumference C to the diameter D of a perfect circle.
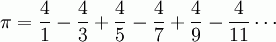
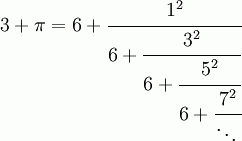
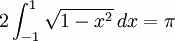
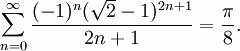
- Several more forms are at this web page and this web page. And there are certainly other much more advanced ways to find the exact value of pi.
Some people continue to calculate more and more decimal places for more accurate approximations of pi. I see someone has posted the first billion digits of pi on the internet. And other people continue to try to memorize a lot of digits of pi as well (although why anyone would want to be able to remember and recite 67000 digits is something I'll never understand).
Stephen.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.