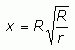A cone with two fruits - Math Central

HOME

Math Central

Quandaries & Queries

Question from Meg, a student:

You have a cone shaped bag. At the bottom of the bag is an orange with
radius r. On top of the orange is a melon with radius R. It touches the
orange and fits snugly in the bag, touching it in a ring around the orange.
Its top is at the same level as the top of the bag. What is the radius of the
cone?

Hi Meg.

We can draw this situation using a simpler two-dimensional geometric sketch:

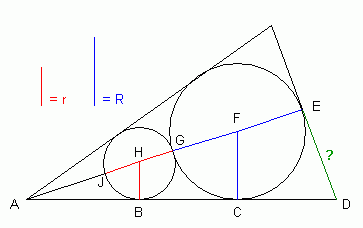
Thus, we are trying to obtain an expression for the length of the green segment in terms of the known blue (R) and red (r) segments. The black lengths are unknown at this time.

First, I hope you recognize that the three triangles AED, ACF and ABH are all similar triangles (they are all right triangles sharing an angle). Thus, the ratios of their sides is common.

|BH| / |AH| = |CF| / |AF| = |ED| / |AD|.

Let x = the length of |ED| and y = the length |AJ|.

Then this triple-equation becomes

r / (r + y) = R / (R + 2r + y) = x / |AD|.

What's |AD|?
It is the hypotenuse of triangle AED, so Pythagoras tells us it is SQRT(x² + (2R + 2r + y)²).

So we can break our triple equation into these two equations:

r / (r + y) = R / (R + 2r + y)

(1)

and

r / (r + y) = x / SQRT(x² + (2R + 2r + y)²)

(2)

So now you have two equations with two unknowns (x and y). It is easiest in this case to solve the first equation for y, solve the second equation for x, then substitute for y in the second equation to complete the solution and come up with an expression for x in terms of just the known values R and r.

There is some long-winded but straightforward algebra which you should work out yourself.

Hint: Don't multiply out squared expressions that you don't have to.

My answer (which I've checked with r = 1 and R = 4), is

Hope this helps,
Stephen La Rocque.

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.