Hi Megan. I've rewritten your question below.

Your question:

There's no obvious way to simplify this.....unless the x + 2 goes into the denominator, in which case it can cancel from the top and bottom of this rational expression. To find out if  x + 2 goes into the denominator, we can use long division.

We won't do your question for you, but we'll do one just as tricky as yours to show you exactly how to solve your own:

Our example:

Does (x - 3) go into this denominator? Let's use long division.

To divide, we first look at the first term: how many times does x go into -4x⁴? It goes in -4x³ times, so we write that above the first term.

Now we multiply what we wrote on top by the numerator x - 3. Then we subtract this from the line above, just like we do when doing long division with numbers. Since -4x³(x - 3) = -4x⁴ + 12x³, we write:

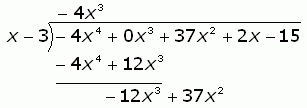
Now we continue this process. If we have a remainder of anything other than zero, then we know that (x - 3)   does not go into the denominator, so we cannot simplify the rational expression any further. But we hope it does....

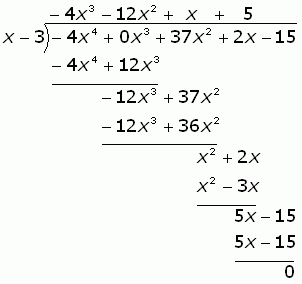
No remainder. So that means  (x - 3) (-4x³ - 12x² + x + 5) = -4x⁴ + 0x³ + 37x² + 2x - 15. So the simplification is just

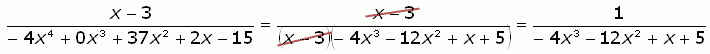
Now you try using long division to simplify your rational expression, Megan.

Hope this helps,
Stephen and Penny.