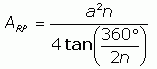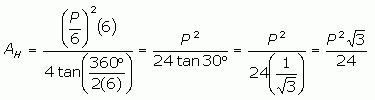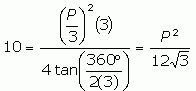Hi Michael.

There are many ways to solve this problem, but I'm going to show you a purely algebriac way. You'll see in this reply to Dana that I derived the equation for any regular polygon's area (A_RP) given its side length a (number of sides is n):

So for a regular hexagon whose perimeter P is known, n=6 and a=P/6, the area of the hexagon is:

[Note: You can see that I've substituted tan 30° with its exact value.]

But we don't yet know what P actually is, except that it is perimeter of an equalateral triangle with area 10 square units. Of course, an equilateral triangle is also a regular polygon, so the same equation applies here. Let's use this to find the value P² which we need in the equation above.

[Again, tan 60° is replaced with its exact value.]

So when we solve this for P², we get

Now we can substitute this value of P² into the earlier equation to find the value A_H that answers the question:

Hope this helps,
Stephen La Rocque.