| |||
| Math Central | Quandaries & Queries |
|
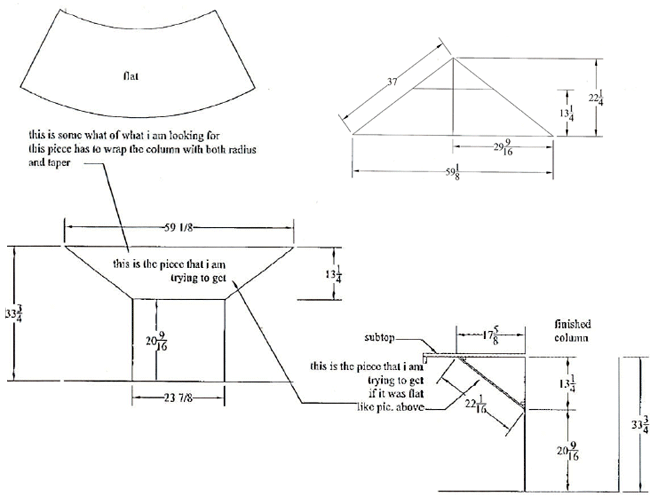
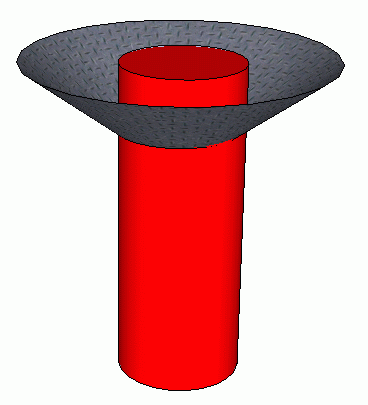
Question from Mike (by fax): I have been trying to get this cone flat so I can build this column. Can you please help me so I can figure this out? Thanks for your help. Mike Mike faxed some drawings:
|
Hi Mike.
|
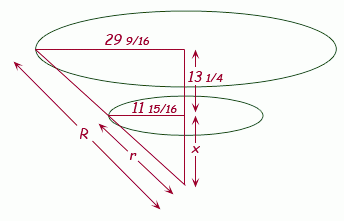
The radius of the column is 11 15/16" . The radius of the circle at the top is 29 9/16". The height of the truncated cone is 13 1/4". This gives the following geometric representation:
|
Due to similar triangles, corresponding side length ratios are equal:
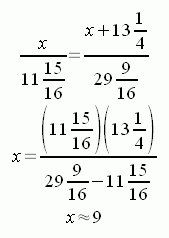
Thus, x + 13 1/4 = 22 1/4, which you had already calculated. Knowing x, we can now calculate the really useful radii r and R by using Pythagorus:
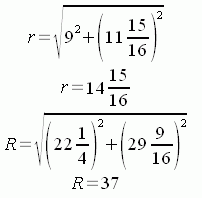
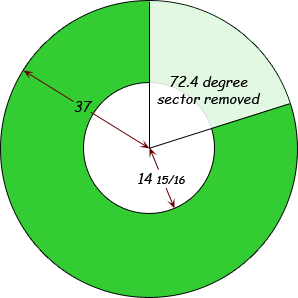
So now we know we are cutting from an annulus with inside radius 14 15/16" and outside radius 37".
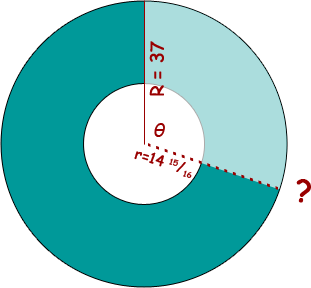
Now we need to consider the portion we must cut.
We know the outside circumference we want remaining is the circumference of the larger radius of the truncated cone. That circumference is the circumference of a circle with radius 29 9/16":
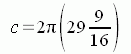
whereas the circumference of the outside of the annulus pattern is
![]()
The ratios of these circumferences is the same as the ratio of the angles through which they turn. That is, since the full circle of the annulus is 360 degrees, we can calculate what the angle θ is by using the common ratios:
![]()
When we solve for θ we get:
![]()
and now substitute in our earlier expressions for c and C to find the value of θ
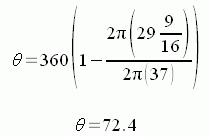
Now we have our pattern: It is a portion of an annulus whose
Cheers, |
 |
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.