| |||
| Math Central | Quandaries & Queries |
|
Question from mini, a student: Find the sample size needed to be 98% confident thata marketing survey on the proportion of shoppers who use the internet for holiday shopping is accurate within a margin of error of 0.02. Assume that the conditions for a binomial distribution are met, and that a current estimate for a sample proportion does not exist. |
Hi Mini,
The confidence limits for the proportion p a binomial distribution is
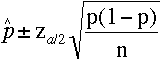
where n is the sample size.
Since you want 98% confidence interval α is 0.02. Since the margin of error is 0.02 the bounds on the confidence interval are ±0.02. Since you have no previous estimate for p take p = 1/2.
Set the bounds on the confidence limits above to ±0.02, substitute the values you know and solve for n.
I hope this helps,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.