| |||
| Math Central | Quandaries & Queries |
|
Question from nhi, a student: |
Hi Nhi.
You didn't send a diagram or indicate where point C or point A are on the diagram, so I will guess that they are as I've indicated in the drawing below:
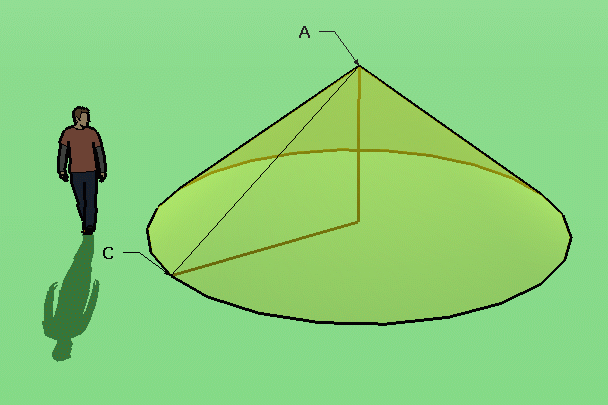
If C and A are elsewhere, I still expect you will learn all you need from this reply to answer your question.
The two important principles here are (1) the shape of the cone doesn't change over time and (2) the rate of sand being added to the cone is constant.
As I've drawn it, the question is asking for the length of the hypotenuse of the right triangle after 7 minutes. Pythagorus informs us that we can get this length by knowing first the radius and height of the triangle at this time.
If the shape of the cone doesn't change, then neither do the measures of the angles of the right triangle inside. This means that the corresponding ratios of sides of the 5 minute and 7 minute triangles are the same:

So the height to radius ratios are constant.
The volume of such a cone can be calculated with the formula
![]()
Since you are given the 5 minute radius and height (call them r5 and h5), you can find the volume after 5 minutes. Since the sand is accumulating at a constant rate, just multiply by 7/5 to find the volume after 7 minutes. Thus the volume at 7 minutes is:
![]()
The volume at 7 minutes can also be written simply in terms of the radius at 7 minutes (r7) and the height at 7 minutes (h7). But since the ratio h7 / r7 = h5 / r5, then h7 = (h5 r7) / r5. So we can write:
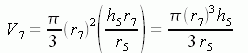
But since this gives us two different expressions for V7 , they equal each other and we can solve for r7 :
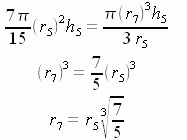
Since these are similar triangles, h7 is the same factor of h5.
Lastly, we can use Pythagorus to find the length from C to A using r7 and h7.
Hope this helps,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.