Hi Ning.

There may be several ways to solve this problem, but I'll show you how I would approach it.

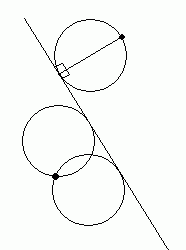
First let's recognize that unless that point given is exactly two radii away from the line, then there must be two different circles that solve the question.

I've drawn these two scenarios on the left for two different points.

Now to begin, let's write the line in slope-intercept form: y = -3x - 19. So its slope is -3. Let's see if the point (0,-3) is above or below the line:

y = -3(0) - 19 = -19

Since -19 < -3, the point is above the line.

So the center(s) of the circle(s) we are looking for must pass through a line parallel to the original line and above it. I'll draw it the parallel line in red:

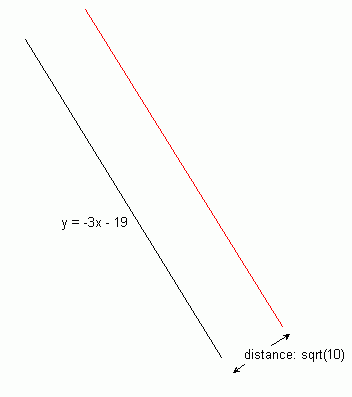
Now to find the equation of the red line, let's look at some similar triangles:

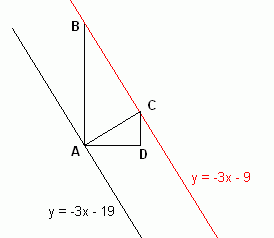
The distance AC in the diagram is sqrt(10). Since the slope of the red and original lines is -3, the perpendicular's slope is 1/3.

That means that AD is 3 times DC. Using Pythagorus, we see that

DC² + (3DC)² = ( sqrt(10) )²

So DC = 1. Now since DC is parallel to AB, angles BAC and DCA are equal and indeed the two triangles ACD and BAC are similar. This means corresponding side ratios are equal as well:

AB/AC = AC/CD so AB = AC² /CD = 10.

Thus, the vertical difference between the two lines is 10 units, so the y intercept of the red line is 10 units higher than the original line. This means the equation of the red line is y = -3x - 9.

Now we know that the point (0,3) is on the circumference of both circle solutions, so the centers of the circles, as well as being on the red line, are also on the circumference of a circle of radius sqrt(10) centered at point (0,3). I'll draw this circle in green:

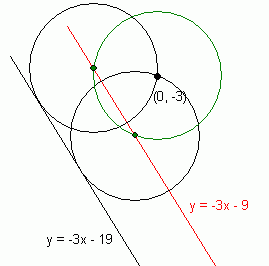
Thus you can see that the centers of the two solution circles are the intersections of the green circle's equation:

x² + (y + 3)² = 10

and the line

y = -3x - 9

Now we must solve this for x (we should get two solutions):

x² + (-3x - 9 + 3)² = 10 reduces to:
x² + 3.6x + 2.6 = 0

And using the quadratic formula, we get x = -1 or -2.6. Putting these values into the equation of the red line, we get the centers of the circle at (-1, -6) and (-2.6, -1.2).

Finally, we can use the standard form of the equation of a circle to substitute in our two centers with radius sqrt(10) to find the equations of the circles:

(x + 1)² + (y+6)² = 10 and (x + 2.6)² + (y + 1.2)² = 10

You can check this by satisfying yourself that both circles contain the point (0,3) and both have a single intersection with the original line.

Stephen La Rocque, Chris Fisher and Penny Nom.