Hi Phonda.

Let's draw a quick sketch to visualize our problem.

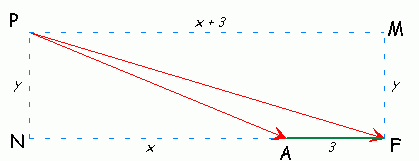
As you can see, there are a couple of right triangles in here - that'll be useful in step 3.

Step 1. Figure out some angles. We are given MPF = 4.8° and MPA = 12.5°. Since PM is parallel to NF, we know therefore that MPF = NFP. We also know by composition that FPA = MPA - MPF. Then, since any triangle's angles total 180°, we can calculate PAF.

Step 2. Use the law of sines to find the lengths of PA and PF. The law of sines tells you that in any triangle (we are looking particularly at PAF here) the sine of an angle divided by the length of the side opposite it is a constant ratio for all the other sides. Since you know one length already (3 miles) and all three angles, you can find the lengths of the other two sides.

Step 3. Use Pythagorus twice to get two equations involving the values x and y. Now you have the lengths of the two hypotenuses of the triangles MPF and PNA. If you write out the Pythagorean formula for each one, you can get two equations, each one involving x and y. Solve both for y².

Step 4. Solve for x. You have two equations with two unknowns. The easiest way to solve this particular pair is to substitute out y² and then solve for x (you may get two answers for x, but you will have to decide if they both make sense; discard any answers that are nonsensical for the context of the question).

Step 5. Solve for y, the altitude of the plane. Using the value of x you obtained, insert it into one of the Pythagorean formulas you determined earlier and solve for y.

Hope this helps,
Stephen La Rocque.