| |||
| Math Central | Quandaries & Queries |
|
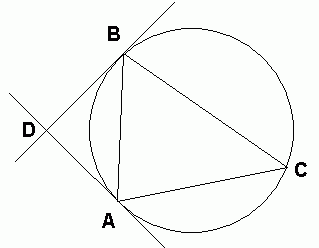
Question from Robin, a student: In a triangle ABC, angle A=75 and B=60. A circle circumscribes the triangle. The tangents of the at points A and B meet in a point D outside the circle. Show that ABD is an isosceles triangle with a right angle at D.
|
Hello Robin.
There are a couple of important circle geometry facts you need to know to solve this question:
- Any two intersecting lines that are tangent to the same circle have the same lengths from the point of intersections to the points of tangency. In your case, this means |AD| = |BD|.
- The measure of the angle from a point on the circumference of a circle that subtends an arc is one half the measure of the central angle (angle from the center of the circle) subtending the same arc. In your case, this means that in the diagram below, m
 ACB = ½m
ACB = ½m AOB.
AOB.
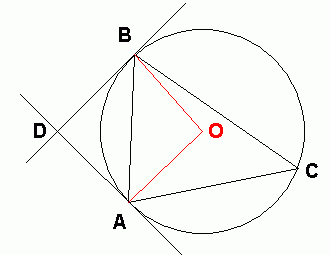
Now you can apply some other facts:
- The angles of all triangles total 180 degrees, so m
 ACB = 180 - 75 - 60 = 45. Using the earlier idea of the circumferential angle being half the central angle, this means m
ACB = 180 - 75 - 60 = 45. Using the earlier idea of the circumferential angle being half the central angle, this means m AOB = 90.
AOB = 90. - Any tangent to a circle is perpendicular to the radius to the point of tangency.
So m DAO = m
DAO = m OBD = 90.
OBD = 90. - The sum of the angles of a quadrilateral is 360 degrees. So m
 BDA = 360 - 90 - 90 - 90.
BDA = 360 - 90 - 90 - 90.
This proves BDA is a right angle.
BDA is a right angle. - Any triangle with two sides the same is isosceles, so triangle ABD is isosceles.
This is the other result that was sought.
Hope this helps,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.