Hi Saher.

I'll help get you started. The first thing I would do is to examine the simpler parts of the function, and there are three I see. I want to know where on the number line each part is positive, negative or zero. I'll mark these with colour:

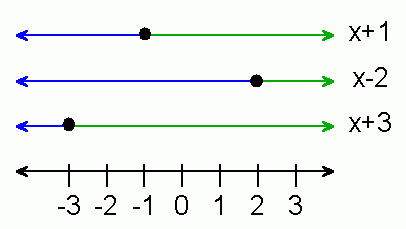As you see, the blue areas denote negative values of the functions labelled on the right side, and green areas are positive.

Values where the function is zero are black (just dots, not lines).

The next step is to combine these functions by looking at the line colours. First we examine the function (x+1)(x-2). Because we are multiplying, anywhere either is zero, the product is zero and anywhere both are the same sign (colour), the product is positive, hence:

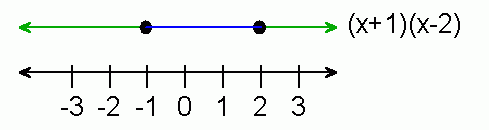
Now we need to divide by the (x+3) number line. A positive number divided by a positive number is positive and so is a negative divided by a negative, anything divided by zero is not allowed, and zero over anything other than zero is zero. So let's mark the not allowed values with red. Thus we combine the (x+3) and the (x+1)(x-2) number lines like this:

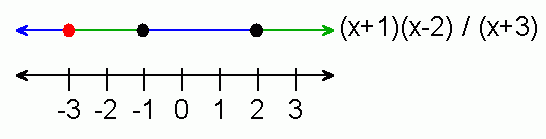
The last step, which I'll leave to you, is to take the square root of this number line.

Remember that you cannot take the square root of a negative number (so anything negative becomes red). And anything that is red in one step is red in all subsequent steps.

The domain of the function f(x) then, is the union of all the areas left on your number line that are not red.

You also mentioned that you are wondering about how to give your answers. Here is an example for you: Let's say I decide that my answer is that the domain is all the values up to and including 100 plus all the values between 200 and 300, but not including 200 or 300. I'd express that answer then as:

(-,100] (200,300)

Round parentheses ( ) mean that the end point is not included and you never include the end points of positive or negative infinity. Square brackets [ ] are used to indicate that that end point is included.

Hope this helps,
Stephen La Rocque.