Hi San.

I'll show you how to solve this question using different figures. Say this is cliff on the Bay of Fundy, where the tides are the highest in the world. At low tide the depth is 2m and at high tide the depth is 19m and the depth y varies according to the function y = 8.5sin(πx/6) + 10.5, where x is the hours after midnight. Let's say it is safe to do the cliff diving when the water is 5 meters deep or more.

If we were to graph this function, we would get this:

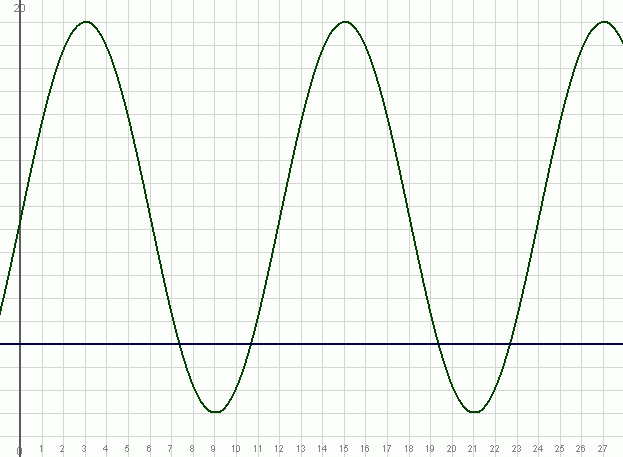
The blue horizontal line is y = 5 meters, so we can see from the graph that it should be safe enough to dive between about 10:30 am and 7:30 pm, but what are these times precisely?

Simply, they are the values of x that correspond to y = 5. Note that I'm only paying attention to the "daylight hours" portion.

So I just solve for x:

5 = 8.5sin(πx/6) + 10.5

-5.5 / 8.5 = sin(πx/6)

arcsin(-5.5 / 8.5) = πx/6

x = (6/π) arcsin(-5.5 / 8.5).

Now it is important to be aware of what arcsin is: your calculator will just tell you -0.70372 radians, but we want two positive numbers here! So we can add 2π easily enough: 5.57946 radians is an equivalent angle.

For the other value though, we need to think about the unit circle. The sine of an angle is the same if you mirror it across the y axis, so the other angle is 5.57946 mirrored across the y axis. Since the y axis is 3π/2   radians down here, that means our angle is 5.57946 - 3π/2 radians on the other side of it. This is 3π/2 - (5.57946 - 3π/2) = 3.84531 radians.

To check this, let's find the sine of both:

sin(3.84531) = -0.6470588 = -5.5 / 8.5 as it should.
sin(5.57946) = -0.6470588 = -5.5 / 8.5 as it should.

Now just multiply by (6/π) and we get x = 7.344 hours and x = 10.656 hours.

So the safe times to dive are between 10.656 hours after midnight and 7.344 hours after noon.

Hope this demonstration helps you with your question,
Stephen La Rocque.