| |||
| Math Central | Quandaries & Queries |
|
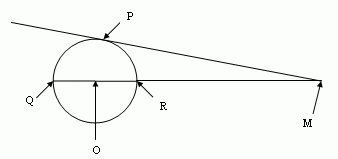
Question from Sean, a student: Let M be a point outside a circle, and let a line through M be tangent to the circle at point P. Let the line through M and the center of the circle intersect the circle in points Q, R. Prove that │PM│2 = │MQ│ x │MR│
|
Hi Sean.
The key is this property of circle geometry:
The angle formed by the tangent to a circle and the radius to the point of tangency is a right angle.
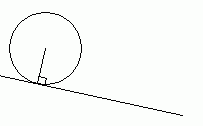
Draw line OP and label your lengths, recognizing that |OQ| = |OR| = |OP| = radius. Then use the Pythagorean Theorem to complete your question with simple algebra.
Hope this helps,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.