 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
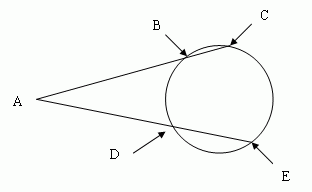
Another question from Sean: Two rays are drawn from the same point A outside a circle, and intersect the circle as shown in the picture. Prove that the measure of angle A is one-half the difference between the measures of arcs BD and CE. I know that I should draw segment DC and look at inscribed angles BCD and CDE, and triangle ACD. After that I am stuck. |
Hi Sean.
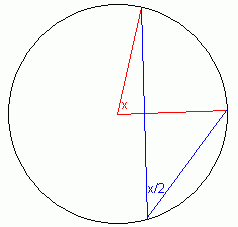The measure of an arc is the measure of the central angle subtending the arc (labelled x on the right).
The same arc subtended by an angle anywhere on the circumference of the circle is half the central angle (labelled x/2 on the right).
So when you draw your line DC (yes, this is the right first step), you know what angle CDE and angle ACD are. You have also created a triangle.
All angles of any triangle add up to 180 degrees. You know angle ACD and can find angle ADC, because it is the supplementary angle to angle CDE. This lets you express angle A, which is what you want.
Stephen La Rocque
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.