| |||
| Math Central | Quandaries & Queries |
|
"The largest possible circle is drawn inside a square. Then the largest possible squuare is drawn inside this circle. What is the area of the inner square as a fraction of the area of the outer square?" This is a question from the Grade 8 Gauss contest and I dont know how to work it out without drawing it. My teacher says it's possible but I still dont get it. Please help!!! |
Hi Confuzzled.
There are probably quite a few ways of doing it. I start with a sketch:
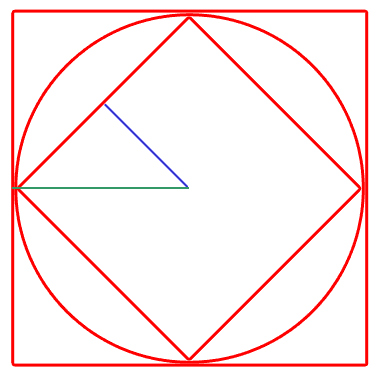
1. Let A be the area of the outer square. Then its side length is what?
2. Then the radius of the circle (in green) is what?
3. Using Pythagorus on the isoceles right triangle, what is the length of the blue line?
4. That makes the side length of the inner square what?
5. So the area of the inner square is?
6. And if you divide that by A, you get the fraction of the bigger square that is also in the smaller square.
Good for you for trying the Gauss contest! It's an excellent way to get new mathematical ideas that you might not encounter in the classroom - or at least not until later years. The Gauss Contest is run by the University of Waterloo and is open to students in Grade VII and VIII across Canada. They also hold other national mathematics competitions every year for older students. You can learn more about them here.
Math Central also has a big list of other math activities and contests offered across Canada, either nationally or in specific parts of the country. These are often free to interested students and everyone is encouraged to check them out.
Stephen La Rocque.>
PS: After I did that diagram, I noticed an even easier way of solving it.
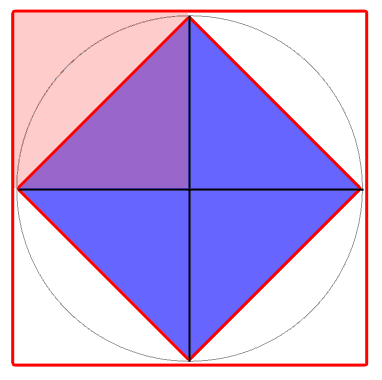
What portion of each quarter of the big square is also in the inner blue square?
(Boy, a whole lot easier, isn't it? Sometimes we don't see the easiest way first.)
![]()
Stephen La Rocque.>
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.