Hello.

Two important things are clear from the question: the height of the corridor is not stated, so it is not meant to be considered. This means the problem is a two-dimensional one. Clearly, using the third dimension of height will allow a longer pipe, but since the height isn't given, we use just the floor of the corridors. Second, the width of the pipe isn't given either. A very wide pipe (say 4 feet wide) would have to be shorter than a narrow pipe. Since the width of the pipe isn't given, we infer that width is not to be considered either.

Here's a sketch of various long pipes coming from one direction or the other. They are all jammed in place except the red one that can make it around the corner.

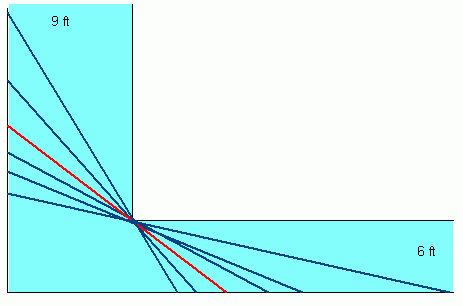
We know that the longest pipe has to squeeze against the inside corner of the junction of the corridors and we know exactly where that junction is, because we know the widths of both corridors. So we can represent any pipe that touches the two outside walls and the inside corner using a simple cartesian graph as below:

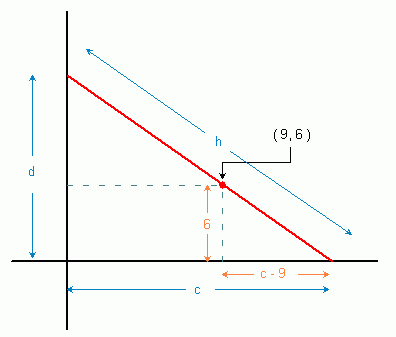
This forms a simple right angled triangle. The base lengths are c and d, the hypotenuse length is h (that's the length of the pipe) and we know the line passes through (9, 6).

Long pipes jam, so really we want the shortest hypotenuse we can find that works in this graph. That will be the longest pipe that can make it around the corner.

Pythagorus tells us that the large triangle has the relationship h² = d² + c² .

By looking at the x-intercept and the point (9,6) we can determine the slope of the red line:

      m = (0 - 6) / (c - 9) = -6 / (c - 9)

The equation of the red line is

y = mx + b
y = (-6 / (c - 9))x + b

but we also know that the line passes through (9, 6) so we can substitute that in for x and y:

6 = (-6 / (c - 9))(9) + b
b = 6 + 2 / (3c - 27)

but b is the y-intercept, which we earlier called d, so if we square this, we get

d² = (6 + 2 / (3c - 27) )²

Now we can substitute this into the Pythagorean equation:

h² = (6 + 2 / (3c - 27) )² + c²

Taking the derivative with respect to c gives us:

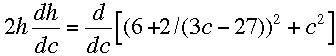
When you set dh/dc to zero, you can find the value of c. Using that, you can find the value of d and h, the length of the pipe.

Hope this helps,
Stephen La Rocque.