Hi Toni.

I'll show you a general way and then a shortcut way to expand this kind of expression.

When you square something, you are multiplying it by itself, so

(2x - 6)² = (2x - 6)(2x - 6)

You have probably heard of the acronym F.O.I.L. which stands for First, Outside, Inside, Last.

Let's simplify it and say the "x" wasn't there. One way to solve (2 - 6)(2 - 6) is to distribute the terms in the first parentheses:

(2 - 6) (2 - 6) = 2 (2 - 6) - 6 (2 - 6) = 2 (2) - 6 (2) - 6 (2) - 6 (-6) = 16, as you'd expect.

Stop here. Notice that we have four products here: the two first terms are multiplied together to make the first product. The second product comes from multiplying the outside terms together, the third product is the inside terms and the fourth product is the last terms.

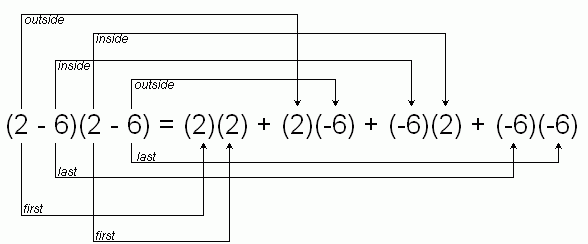
It works the same with variables involved. For (2x - 6)(2x-6), you multiply the first terms together and add the product of the outside terms, etc.:

(2x - 6)(2x - 6) = (2x)(2x) + (2x)(-6) + (-6)(2x) + (-6)(-6)

Now using BEDMAS, we have 4x² - 12x - 12x + 36 = 4x² - 24x + 36.

When you get comfortable with FOIL, you can do it really fast in your head.

Shortcut. Now for a shortcut that works only for squared terms like (2x - 6)² .

Notice that we had two copies of -12x up above? This duplication will always happen with a squared term, because the product of the inside terms is always the same as the product of the outside terms when you are squaring it.

So I know the answer to (2x - 6)² is the first term squared plus twice the product of the first and last term plus the last term squared. That is:

(2x - 6)² = (2x)² + 2(2x)(-6) + (-6)² = 4x² -24x +36. The same answer as before.

Always be careful of the minus signs!

Hope this explanation helps.
Stephen La Rocque.