Tracy, we have three responses for you...

Hi Tracy.

The area of a shape is always equal the sum of the area of all its parts. That means we can carve the pentagon into smaller shapes we can easily find the area of and add (or multiply).

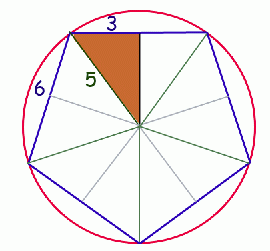
If we draw the radius to all the corners in green , the pentagon in blue and the circle in red, we get the diagram on the left.

I've also drawn a line from the center of the circle to the midpoint of each side of the pentagon. Because it is the midpoint, it meets the side in a right angle, so it forms congruent triangles. I think you can see that by symmetry, there are ten congruent right triangles here.

Now you can use the Pythagorean Theorem to find the height of the right triangle. Then use that to find the area of the right triangle. Finally, multiply by the number of congruent triangles in the pentagon.

Hope this helps,
Stephen La Rocque.

Hi Tracy,

The area of the regular pentagon will be the same as the sum of the areas of the five identical isosceles triangles you can form by drawing in the radii to the vertices of the pentagon.

Now you can see that you know the lengths of all three sides of each individual triangle.

Heron's Formula can be used to determine the area of the triangle when you know all three sides:

where a, b, c are the sides and s=(1/2)(a+b+c)

You could also determine the size of the central angle (C) which is also the vertex angle of each triangle formed. and then use Area=(1/2)ab*sinC.

Just remember that after you find the area of one triangle, you must multiply by 5 to get the area of the entire pentagon.

This is just a couple of the ways in which this problem could be solved.

Hope this helps, Leeanne

Tracy,

The area is 1/2 base times altitude of the triangle that consists of one of the pentagon's sides and the radii to the two endpoints of that side.  You multiply that area by 5 for the area of the pentagon.  I suppose that you can use 6 as the length of the side, but the side really has length 10*sin (36 degrees), which equals about 5.8779.  The altitude (which is the distance from the centre of the pentagon to the side) is 5*cos (36 degrees), (which equals about 4.0451).  (If you use the Pythagorean theorem with a triangle whose sides are 5, 5, and 6, the altitude to the base is then 4 instead of the more exact 4.0451.  In fact, the triangle made up of half a side, altitude and radius is a 3-4-5 right triangle.)

Chris