Hi Trish. That would take me a long time to list!

I think you meant to ask how many such combinations there are of 6 numbers chosen from a group of 36 numbers, where you can't pick the same number twice and where the order you choose numbers in doesn't matter. This is the way lotteries usually set things up.

The mathematical way of expressing this value is ₃₆C₆ (we read it as "36 choose 6").

The value of a combination of the form _nC_k is:

The exclamation point means "factorial" which means take the number to the left of the exclamation point and multiply it by all the positive whole numbers smaller than itself. So 4! would be 4321 (although we can leave off the x 1 of course).

For your question, we set n = 36 and k = 6 and work it out:

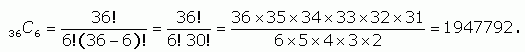
So this calculation tells us that there are almost 2 million different lottery combinations.

Stephen La Rocque.>