Hi Vineet.

I'm not certain whether you are wondering:

1) Why does the Pythagorean Theorem work? or

2) Why does squaring the numbers suddenly made things go from a less than to an equal to?

So I'll try to answer both questions.

Why does the Pythagorean Theorem work?

Let's say you have a right-angled triangle whose hypotenuse length is h and whose other sides are a and b, where a≤b (a is shorter or the same length as b). This can describe any right angled triangle.

Now let's draw four of them with a square in the middle as follows:

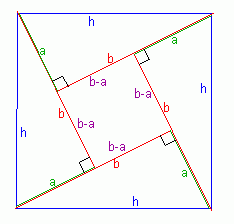
Now you can see I've created a square with h on each side. This means the area of the whole big diagram is h² . But you have the same area as if you add up the areas of the central small square and the four triangular areas. The area of a triangle is half the base times the height, so the area of one triangle is ½ab. The central square has the area of (b-a)² . This means that:

h² = 4( ½ab ) + (b-a)²

so let's solve this:

h² = 2ab + (b² - 2ab + a²)

h² = a² + b²

And this is the Pythagorean Theorem we've just proven!

Why does squaring the numbers suddenly made things go from a less than to an equal to?

Let's look at the two equations we have:

h < a + b and

h² = a² + b²

Remember that these are all length measurements, so they are all positive.

What happens if we square both sides of the inequality? We get:

h² < (a + b)²

that's

h² < a² + 2ab + b²

but if h² = a² + b² for a right triangle, then we can substitute this for h² in the inequality:

a² + b² < a² + 2ab + b²

simplify it and you get

0 < 2ab

which is certainly true since a and b are both positive numbers.

So this is showing how squaring the sum of two positive numbers is larger than the sum of the squares of the same two numbers. That means that even though the unsquared condition might be a less-than relationship, the squared condition can be equal-to in a right triangle.

Hope this helps,
Stephen La Rocque.