Hi William.

I've drawn the scene, forces and force components below.

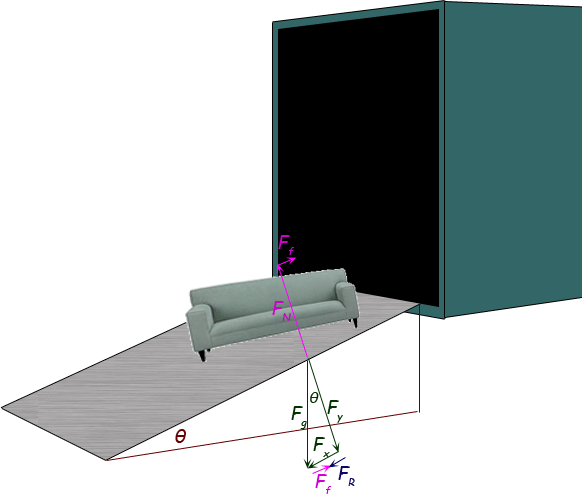
First, I hope you can recognize that the angle θ for the ramp is the same as the angle θ between the force due to gravity (F_g ) and its component perpendicular to the ramp (F_y ). This is due to similar triangles.

Now, you want the co-efficient of kinetic friction and that is μ in the equation F_f = μ F_N, where F_f is the force of friction and F_N is the normal force. Thus we have:

μ = F_f / F_N

You know that the magnitude of the normal force F_N is the same as the magnitude of the force F_y (otherwise the couch would be sinking into the ramp or levitating!) But right triangle trigonometry tells us that F_y = F_g cos θ. So:

μ = F_f / ( F_g cos θ)

I've transcribed the frictional force from the top of the diagram to the bottom so you can see how it has to add up. The resultant force (giving rise to the acceleration of the couch) is F_R. This is a result of the component of the gravitational force that is parallel to the ramp (F_x ) and the frictional force that opposes it (F_f ). So (using magnitudes only), F_f = F_x - F_R . This means:

μ = (F_x - F_R ) / ( F_g cos θ)

Again using standard right triangle geometry, we know that F_x = F_g sin θ, so:

μ = ( F_g sin θ - F_R ) / ( F_g cos θ)

By Newton's Law, the resultant force F_R = ma_R , where a_R is the resultant acceleration. Thus,

μ = ( F_g sin θ - ma_R ) / ( F_g cos θ)

And lastly, F_g is simply mg, so the mass cancels out and our final equation is:

μ = ( g sin θ - a_R ) / ( g cos θ)

So from here, you have all the values you need. Note that the question says the resultant acceleration is 0.70 meters per second [sic]. Meters per second isn't an acceleration, so something is wrong with the question. My guess is this is a typo and it should say 0.70 meters per second² .

Hope this helps,
Stephen La Rocque.