|
 |
|
Subject: Finding the side length of a regular n-gon Hello. My name's Shannen and I'm an eighth student. I got an assignment from my geometry teacher but I don't understand how to do the problem or what certain letters stand for. The problem is: Find the length of each side of a regular n-gon when a=80ft, n=20ft, and A is approx. 20,000 square feet. What do "a" and "n" stand for and how do I find the side length of an n-gon? Thanks in advance!
|
|
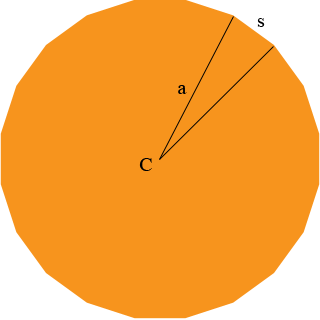
Shannen, A regular n-gon is a polygon with n sides of equal length and with all the interior angles equal. Thus , for example a regular 3-gon is an equilateral triangle and a regular 6-gon is a regular hexagon. Hence in your problem I think n = 20 not 20ft. So you have a regular 20-gon. I tried to sketch one but unless you make it very large it just looks like a circle.
My first thought was that a = 80 ft is the distance from the centre C of the 20-gon to one of its vertices as in the diagram. If you draw the circle with centre C and radius 80 ft its area is
which is just larger than the 20,000 sq ft area of the 20-gon, thus I think I was correct, a = 80 ft is the distance from the centre C of the 20-gon to one of its vertices. Now can you find s, the length of a side of the 20-gon? Penny |
 |
 |
 |